Tasha's devlog

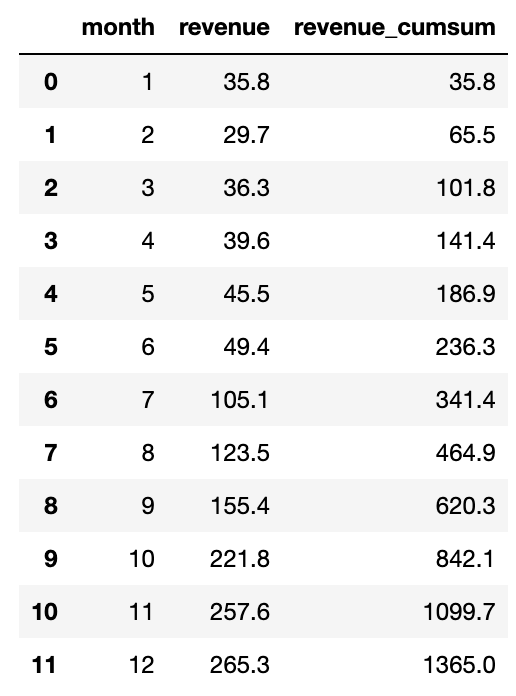
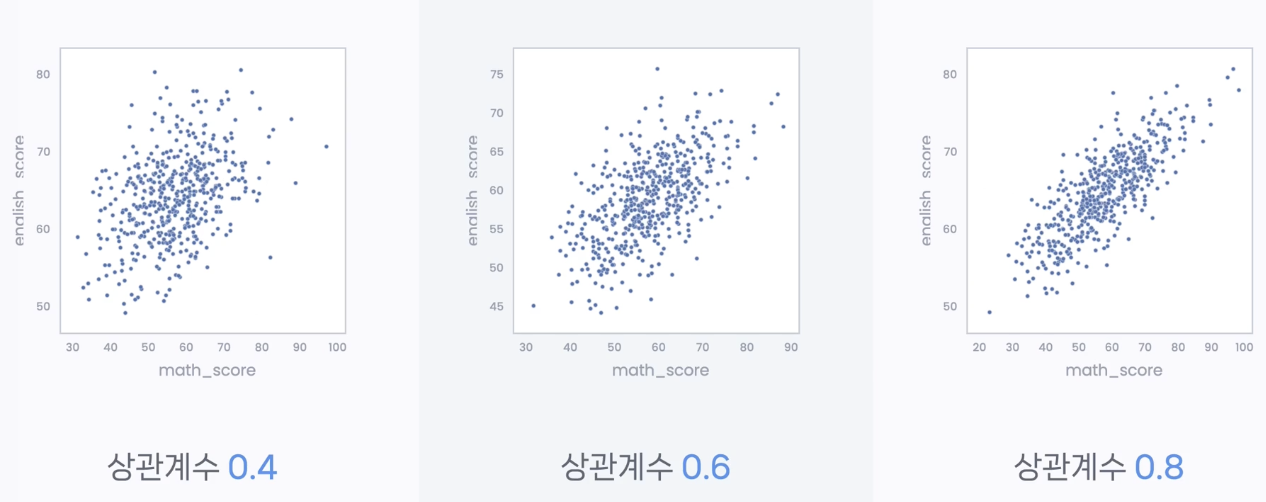
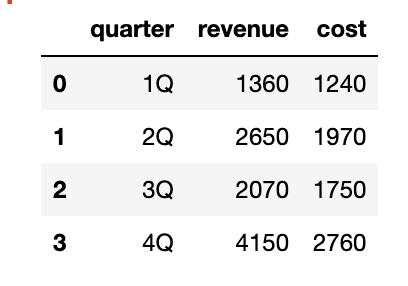
# 코드잇 데이터 사이언스 강의 듣는 중  - . cumsum() --> cumulative sum 누적 합- 예를 들어, 수입의 누적 값을 확인하고 싶을 때 등에 쓸 수 있음. df['revenue_cumsum']= df['revenue'].cumsum()df - 진짜.. 너무 편한듯.. ㅎ          - 플롯으로 변경 추이를 한 눈에 확인할 수도 있음. df.plot(x='month', y='revenue_cumsum') df.plot(x='month', y='revenue_cumsum', kind='bar') - . cumprod() --> cumulative  product 누적 곱- 예를 들어, 연간 금리에 따른 만기액 같은 계산이 가능해짐.  +..ㅎ 내가 진짜 학생 때 제일 싫어했던....

# 코드잇 데이터 사이언스 강의 듣는 중 - 편차 제곱의 합의 평균  1) 편차의 합은 0이 되기 때문에 제곱해서 다 양수로 통일하는 것2) 편차가 큰 값들을 더 부각시키기 위함df['height'].var()#52.92330276553103  - 편차 제곱의 합의 평균에 루트를 씌운 것.- 분산을 구할 때 제곱을 했기 때문에 이것을 다시 원래의 단위로 맞춰 주는 것 df['height'].std()#7.2748403945056435   - but, 위의 공식은 모집단의 값을 구하는 공식이고, 표본을 구할 때는 값이 달라짐.+ 아 그냥.. 공식을 써주지.. 그래야 시그마랑 구분하자나.. --> n이 아닌 n-1로 나눠서 평균을 구하는 것- 표본은 결국 모집단을 추정하기 위함인데, - n으로 나누면 과소..

# 코드잇 데이터 사이언스 강의 듣는 중 - 원래 측정하고 싶던 전체 집단 - 예, 한국 대학생 전체  - 모집단에서 측정가능한 일부만 추출한 집단- 예, 00대학교 심리학과 학생 전체 (200명)- 데이터 요약 및 핵심적인 특징 파악- 예, 평균, 편차, 분산, 상관 등  statistics>- 표본을 기반으로 모집단을 추론하는 것- 예, 회귀, 분산 등 +++ - 희한하게.. 데분 쪽에서는.. 변수 종류를 제대로 설명을 안함.. 왜이러는 거임..?- 이렇게 구분해 놓는 것이 통계 돌릴 때 어떤 분석이 가능하고 어떤 것이 아닌지 알기 편함. - 이산형discrete 변수..이름이 기억 안 나서 자꾸 그 불리안......하다가 ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ찾았음.. - 예전에는 불리안을 몰랐는데 이젠 디스크리트를..

# 코드잇 데이터 사이언스 강의 듣는 중 - 서로 관련이 있는 집단들을  묶어서 분석하는 것- sns.clustermap() - 강의에서는 상관이 있는 것들을 묶는 예제를 보여줬는데, 실제로는, 상관.... 보다는 변수들 간의 관계나 값의 분포 차이에 따라서 군집을 나눔.  + 군집분석은 data driven 이기 때문에 일반화 하기가 어렵다는 문제가 있지만, 확진적 요인 분석 CFA 과 잠재 프로파일분석 LPA으로 논문을 썼기 때문에 흥미로운 결과를 많이 뽑아낼 수 있다고 생각하는 편이다.  - 필요한 칼럼만 분리하고.interests = df.loc[:, 'History':'Pets']interests.head() - 상관을 아예 변수에 넣음.corr = interests.corr()corr - 역사..

# 코드잇 데이터 사이언스 강의 듣는 중  - 여러 상관 계수가 있지만, 피어슨 Pearson 상관 계수를 많이 씀. 1) 범위: -1 2)  피어슨 Pearson 상관 계수 = 0 --> 상관이 없음. 3)  피어슨 Pearson 상관 계수 = +- 1 --> 강한 상관4) 1 > 피어슨 Pearson 상관 계수 > 0 : 정적 상관; x가 커지면 y가 증가        5) -1 피어슨 Pearson 상관 계수        ++++ --> 피어슨 상관계수 --> x,y의 공분산 값을 각각의 표준편차의 곱으로 나눠준 것  공분산 covariance> --> 각 값의 편차끼리 곱한 값을 n수로 나누어 준 것으로 변수의 관계의 방향성과 강도를 측정할 때 사용 가능함.  - 즉, 같이 움직이는 경향성임. 편..

# 코드잇 데이터 사이언스 강의 듣는 중 - data에 따라서 대표치를 어떤 것으로 볼 지가 달라짐.- outlier가 크면, median은 mean보다 outlier의 영향을 덜 받기 때문에 사용- but, median은 전체 값의 분포가 달라져도 같을 수 있지만, mean은 값에 영향을 받기 때문에 median이 다 같으면 mean 더 좋은 대표치가 됨.  --> numerical(수치형) data는 mean, median, mode를 구할 수 있음 - but categorical(범주형) data는 mean, median을 구할 수 없기에 mode가 대표치가 됨.  + 수치형 데이터는 1) 이산형데이터 (값이 정확히 떨어짐; 오늘 마신 아메의 갯수) 와2) 연속형 데이터 (값이 정확하지 않음; 추정..

# 코드잇 데이터 사이언스 강의 듣는 중  - 확률밀도함수: 값들이 어떻게 분포되어 있는지 보여주는 것. - 분포는 히스토그램과 비슷함. 히스토그램 막대를 무한으로 늘리면 나타나는 것과 비슷함. - but, 히스토그램은 각 구간마다 값이 몇 개 있는지 셌다면, PDF는 각 구간이 전체에서 차지하는 비중(확률)을 보는 것.   - 데이터 셋의 분포를 나타냄. - 특정 구간의 확률은 그래프 아래 그 구간의 면적과 동일함. - 그래프 아래의 모든 면적의 합 = 1 - 연속형 데이터에서 특정 값이 일어날 확률은 0%- 즉, 키가 174.5 일 확률은 0임. coz, 174.50000001 일 수도 있고, 몇 명을 모아도 저 값의 딱 떨어질 확률은 0에 가까움- 주사위 숫자나 동전 면의 확률과 달리,키, 몸무게,..

#코드잇 데이터 사이언스 강의 듣는 중#데이터 사이언스 Toolkit  renewal 버전과 이전 데이터 시각화 강의가 섞인 정리 - numpy처럼 matplotlib을 메소드로 쓸 수도 있지만, Pandas 플랏이 어차피 plt를 끌어다가 쓰는 것이라서 더 간단하게 사용가능. import pandas as pdimport matplotlib.pyplot as pltsales_df = pd.DataFrame({ 'quarter' : ['1Q', '2Q', '3Q', '4Q'], 'revenue' : [1360, 2650, 2070, 4150], 'cost' : [1240, 1970, 1750, 2760]})sales_df#plt plot을 따로 이용plt.plot(sales_df['qua..