https://www.youtube.com/watch?v=kYB8IZa5AuE&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=3
이번에는 엘리스 해당 파트 듣기 전에 이걸 먼저 듣고, 넘어가보려고 한다.
Unfortunately, no one can be told what the Matrix is. You have to see it for yourself.
— Morpheus
(Surprisingly apt words on the importance of understanding matrix operations visually.)
- 매트릭스 영화에서 나온 대사인 건데.. ㅎ 진짜 꼭 시각적으로 봐야 한다.
안 그러면 이해가 안돼.. 일단 나는..
- 그냥 외우지 말라고 하는데 일단 가능할 지 봅시다 ㅎ

[선형 변환 Linear transformation]
- 변환 = 함수 f(x) -> 입력값을 받아서 출력하는 것
- 선형대수학에서 한 벡터를 입력 받아서 다른 벡터로 출력하는 변환을 좋아함 L(V)

- 같은 의미인데 다른 단어를 사용하는 이유는 입-출력 관계를 특정한 방식으로 시각화하도록 하기 위함
- 벡터를 이해하기 가장 좋은 방법은 운동movement을 통해서임.
- 아래 인풋 벡터의 화살표가 아웃풋 벡터로 "이동"한다고 생각하면 편함.

- 아래처럼 확장해서 생각해볼 수도 있음. 모든 입력 가능한 벡터가 출력 벡터를 향해 움직인다.

- 그런데 저러면 머리가 아프기 때문에 화살표의 끝을 하나의 점이라고 생각하면 쉬움.
- 아래의 점이 다음 사진처럼 이동한다고 생각하면 편함.

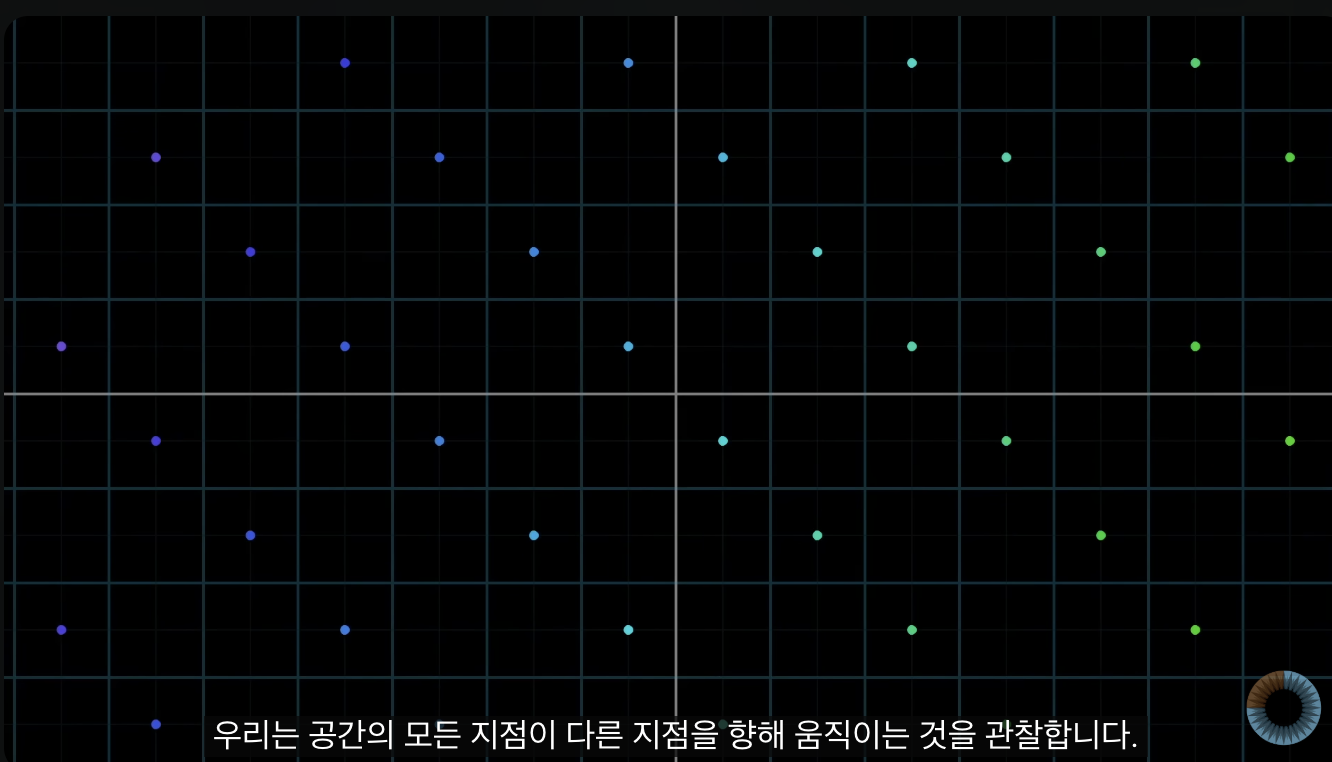
- 사실상 2차원 내에서 점, 선, 면이 다 되는 것임.


- 굉장히 다양하게 변화할 수 있지만, 대수학에서는 몇몇으로 형태가 제한됨.
- 그 중에 하나가 선형 변환임.
[선형변환의 2개의 속성]
1. 모든 직선은 곡선 없이 직선으로 유지됨.
2. 축의 원점은 그대로 유지되어야 함.



- 직선만 볼 때는 변화하는 것 같지 않을 수 있지만, 대각선diagonal도 확인해줘야 함.

- 일반적으로 선형변환은 격자선을 평행하게 유지하고 동일한 간격으로 배치함.

- 축의 원점을 중심으로 한 회전은 가능

- but, 어떻게 복잡한 움직임을 구현해낼것인가? 어떤 값을 입력해야 하는 가의 문제가 있음.

- 이럴 때는 i^과, j^의 위치만 알고 있으면 됌.


- 격자를 그대로 오른쪽 밭향으로 틀었음. 보면 뒤에 그리드가 원래는 파랑/흰색 선과 일치했었음.
- 핵심은 격자선이 평행하고 동일한 간격으로 유지된다는 것임.

- 이렇게 되면 i^, j^을 스케일링하여 변행해도 똑같게 할 수 있음.
- 보면 지금 변형된 값들은 방향이랑 위치만 바뀐 거임.
-> i^과 j^이 된 것과 정확히 동일한 벡터의 선형 조합이 된 것임.

=> i^, j^이 어디로 갈지에 따라서면 v가 어디로 갈지 추론할 수 있음.
- 이게 강연자가 원본 그리드 사본을 배경에 보관하는 이유라고 함.

- 결국 기저벡터에 선형 결합이 새로운 벡터 값이 됨 => 선형 변환임.
- 이러면 정확하게 변형하는 것을 보지 않고도 i^, j^이 가르키는 지점을 알 수 가 있음. => 명백하게 특정 지점을 가르키기 때문


- i^, j^의 값을 알면 어떤 벡터가 들어오더라도 어떻게 변형될 지를 알 수 있음.
- 2차원 선형변환은 4개의 숫자만 알고 있으면 됨.
- i^ 의 xy좌표와 j^의 xy좌표만 알고 있으면 가능함.
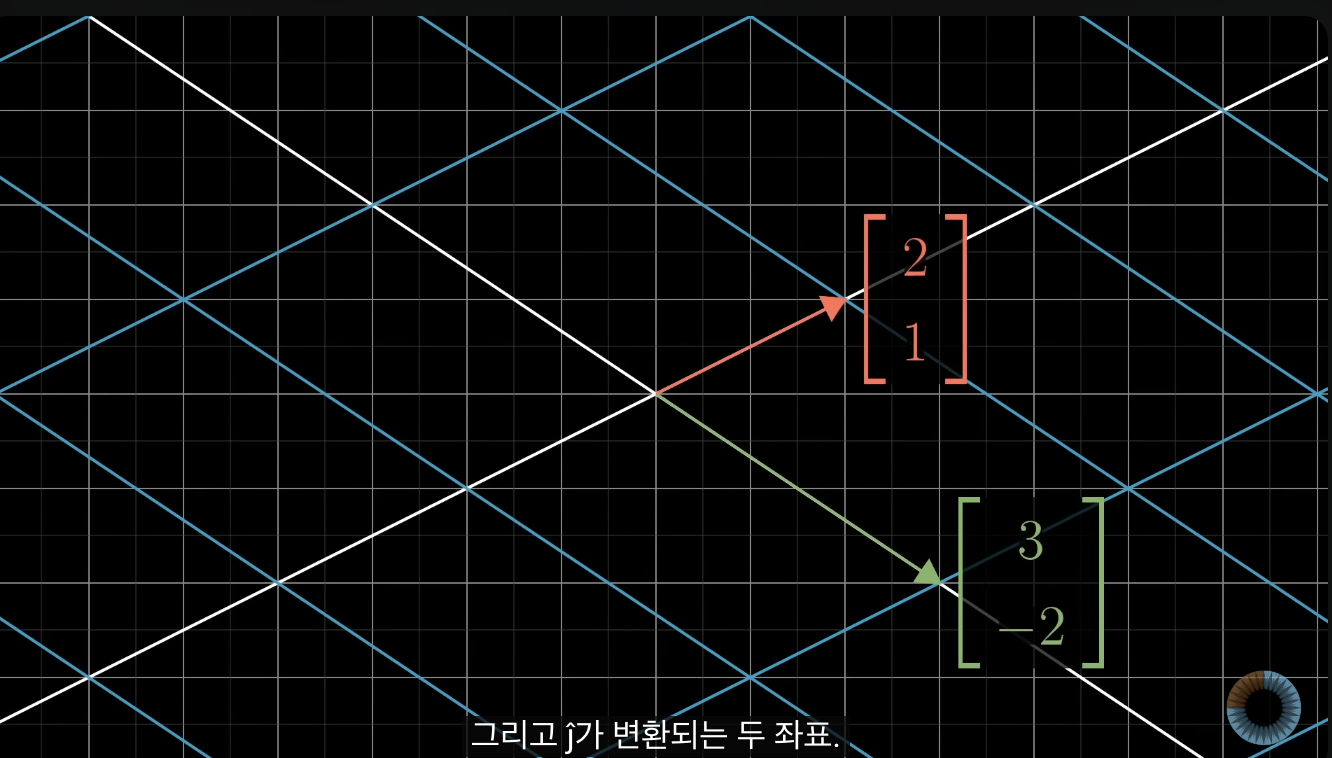


- 마찬가지임 2x2 매트릭스 그리드로 만들어도 새로운 거 하나 더 넣어주면 됨.

- 일반적인 경우
- 공식은 아래가 됨. 선형 곱의 형태로 쓸 수 있음.

- but, 반드시 원리를 이해할 것.
- 1열은 i^이고 2열은 j^이 되는 것임.
- 각각 x와 y의 기저 벡터이고 새로 들어오는 벡터 값을 곱해서 스케일링을 하여
새로운 좌표 값을 구하게 되는 것임.

- 90도 시계 반대 방향으로 돌렸을 때 예시

- 90도 돌리고 어떻게 되는 지 궁금하면 그냥 새로운 벡터 값을 곱해주면 됨.

[전단 Shear]
- i^은 그대로지만 j^은 1,1 로 변경 됨.

- 왜곡이 주어진 벡터를 어떻게 변환하는 지 찾는 것은 이 행렬을 곱하면 됨.

변형이 있는지 알아보고자 할 때 어떻게 할 수 있는지.

- i^과 j^을 격자선을 평행하고 간격을 동일하게 유지함.

- 선형 종속은 하나는 다른 하나의 스케일된 버전임을 의미하기에
선형변환이 전체 2차원 공간을 압축하여 하나의 선으로 만들어 압축하는 것을 의미함.
=> 1차원 스팬
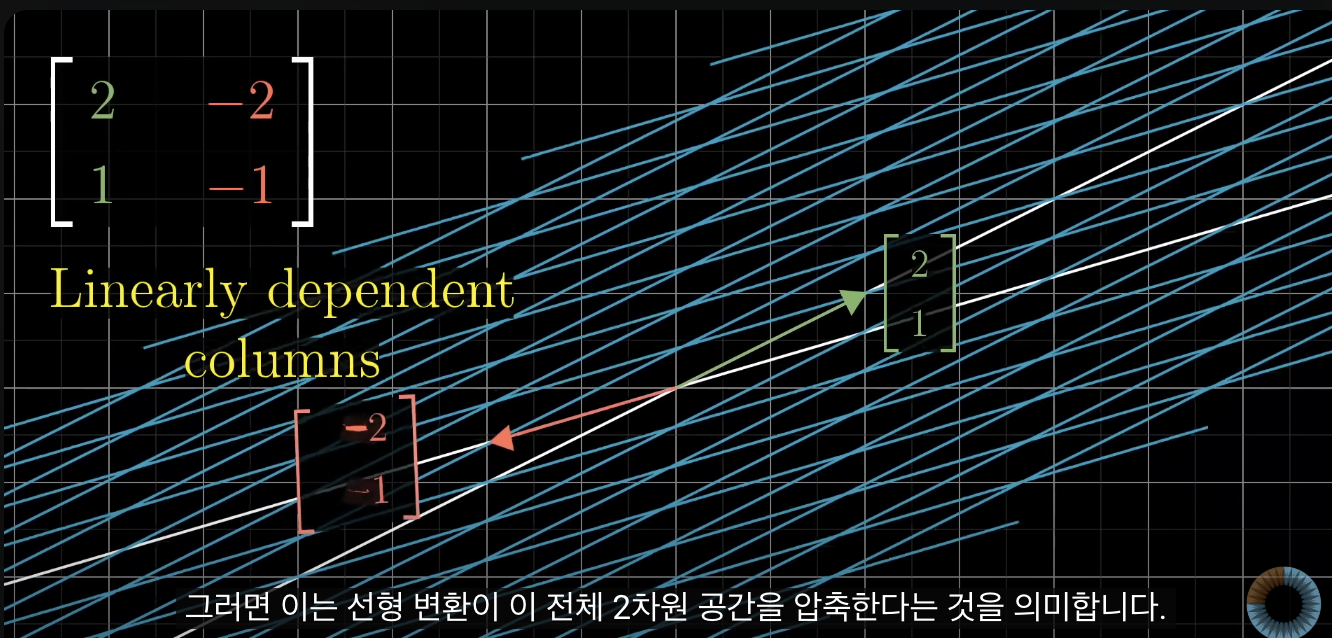

===> recap
- 선형변환은 우리의 주변의 공간을 움직이는 방법임.
- 격자선이 평행을 유지하고 간격이 동일하게 유지되도록 하며, 축의 원점도 일정하게 유지됨.
- 이러한 변화는 몇 개의 숫자로 설명 가능
- 매트릭스 열로 각 기저벡터가 변환 될 좌표를 나타냄
- 행렬-벡터 곱셈은 단지 계산하는 방법일 뿐임 -> 이 변환이 벡터에 어떤 영향을 미치는 가
- 그림을 볼 때마다 공간의 변형으로 해석할 수 있게 되면 다음 챕터들을 잘 이해할 수 있음.
'AI > Linear Algebra, Math' 카테고리의 다른 글
| [elice 머신러닝] 선형변환과 행렬 분해 (0) | 2025.05.04 |
|---|---|
| [elice 머신러닝] 랭크를 활용한 선형 방정식 (0) | 2025.05.04 |
| [Essence of linear algebra] ch2. Linear combinations, span, and basis vectors (0) | 2025.05.04 |
| [Essence of linear algebra] ch1. Vectors (0) | 2025.05.03 |
| [elice 머신러닝] 행렬의 특성 구하기(rank, 기저벡터, column space, null space) (0) | 2025.05.03 |