728x90
*elice 강의안
- 일단 앞 파트 완벽하게 이해 안됐는데.. 그때까지 미룰 수는 없으니깐 우선 끝내자




- p보다 약간 큰 것의..기울기..?
- 진짜 설명 너무 못 함.
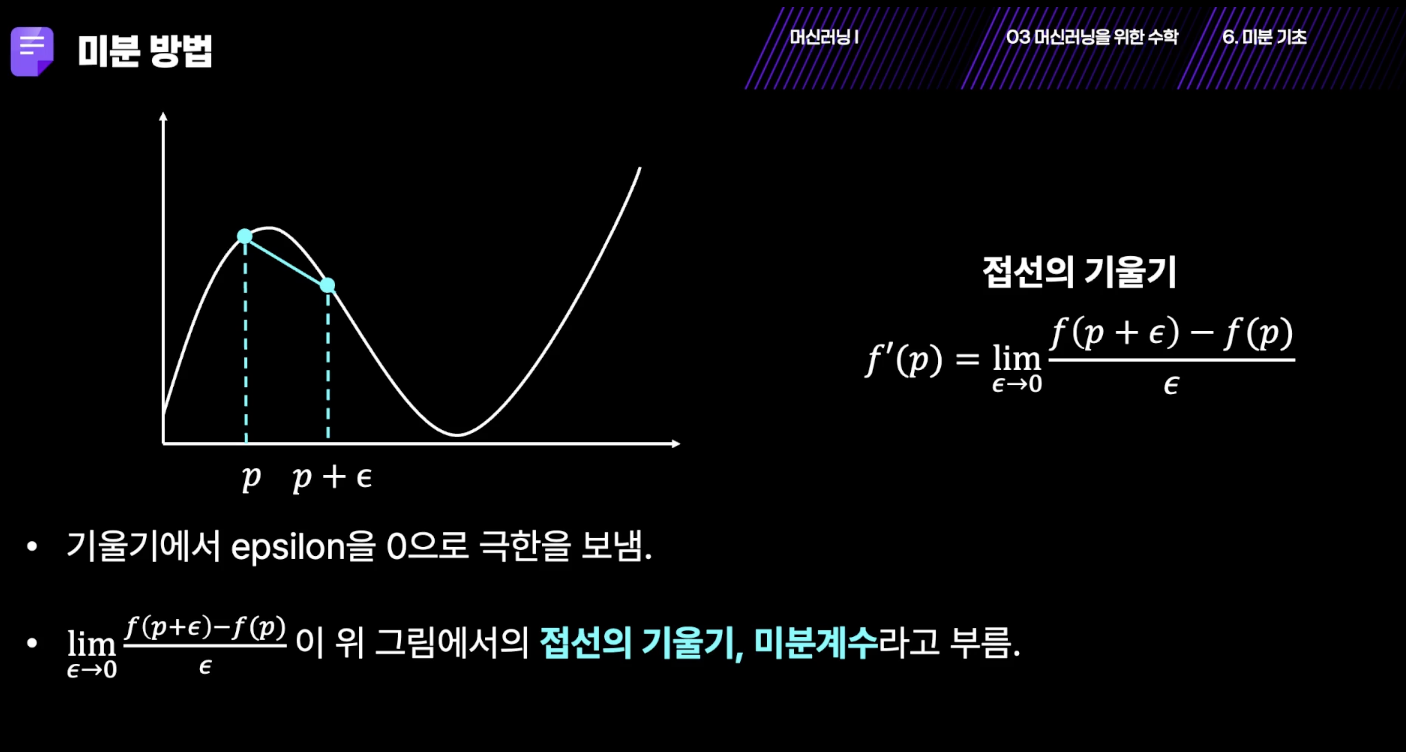
- 접선의 기울기와 평균 기울기를 가깝게 만드는 것

- 곱셈과 덧셈에 닫혀 있음.


- h에 속미분이 나온대.... 돌겠네..

[편미분]








- [x 미분 값, x] 가 답임..

[다항 함수 미분]
- 미분 너무 오랜만인데.. 함수 쓴 거랑 직접 수식 쓴 값이랑 비교하는 코드임.
import numpy as np
import sympy
from sympy import *
# sympy 변수 설정
x, y = symbols('x y')
# f(x) 함수 초기화
sym_f = sympy.expand((x-2*y)**2)
print("Before differentiation : {}".format(sym_f))
# Sympy 계산 함수
sym_d_f_x = sympy.diff(sym_f, x)
print("Sympy differentiation by x : {}".format(sym_d_f_x))
sym_d_f_y = sympy.diff(sym_f, y)
print("Sympy differentiation by y : {}".format(sym_d_f_y))
# 도함수 수식 함수
def d_f_x(x,y):
return 2*x-4*y
def d_f_y(x,y):
return-4*x+8*y
# 증분을 사용한 함수
def f_x(x,y):
return (x-2*y)**2
def d_f_x_incremental(x,y):
x_incremental = 0.00001
return (f_x(x+x_incremental, y) - f_x(x,y)) / x_incremental
def d_f_y_incremental(x,y):
y_incremental = 0.00001
return (f_x(x, y+y_incremental) - f_x(x,y)) / y_incremental
# (1,1)에서 x로 편미분한 값을 구현한 2가지 방식으로 출력
print("d_f_x(1,1) = {}".format(d_f_x(1,1)))
print("d_f_x_incremental(2,1) = {}".format(d_f_x_incremental(1,1)))
# (1,1)에서 y로 편미분한 값을 구현한 2가지 방식으로 출력
print("d_f_y(1,1) = {}".format(d_f_y(1,1)))
print("d_f_y_incremental(2,1) = {}".format(d_f_y_incremental(1,1)))728x90
반응형
'AI > Linear Algebra, Math' 카테고리의 다른 글
| [elice 머신러닝] 통계분석 (0) | 2025.05.04 |
|---|---|
| [elice 머신러닝] 확률 변수와 조건부 확률 (0) | 2025.05.04 |
| [elice 머신러닝] 선형변환과 행렬 분해 (0) | 2025.05.04 |
| [elice 머신러닝] 랭크를 활용한 선형 방정식 (0) | 2025.05.04 |
| [Essence of linear algebra] ch3. Linear transformations and matrices (1) | 2025.05.04 |