https://www.youtube.com/watch?v=rHLEWRxRGiM&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=5
Lisa: Well, where’s my dad?
Frink: Well, it should be obvious to even the most dimwitted individual who holds an advanced degree in hyperbolic topology that Homer Simpson has stumbled into… (dramatic pause) the third dimension.
Lisa: 음, 우리 아빠는 어디 계세요?
Frink: 음, 고차원적인 위상수학(하이퍼볼릭 토폴로지)에 정통한 사람이라면, 아무리 멍청한 사람이라도 호머 심슨이… (극적인 정적)
…제3차원으로 들어가 버렸다는 걸 알 수 있지요.
..? 처음에 뭔소리지? 우리가 사는 게 3차원이잖아? 하면서 gpt에게 물어보니 그게 바로 핵심 유머라고 하였다..ㅎ
심슨 가족의 프링크 교수가 굉장히 쉬운 말을 어렵게 하는 교수라고 하면서 말이다.
[3차원 선형 변환]
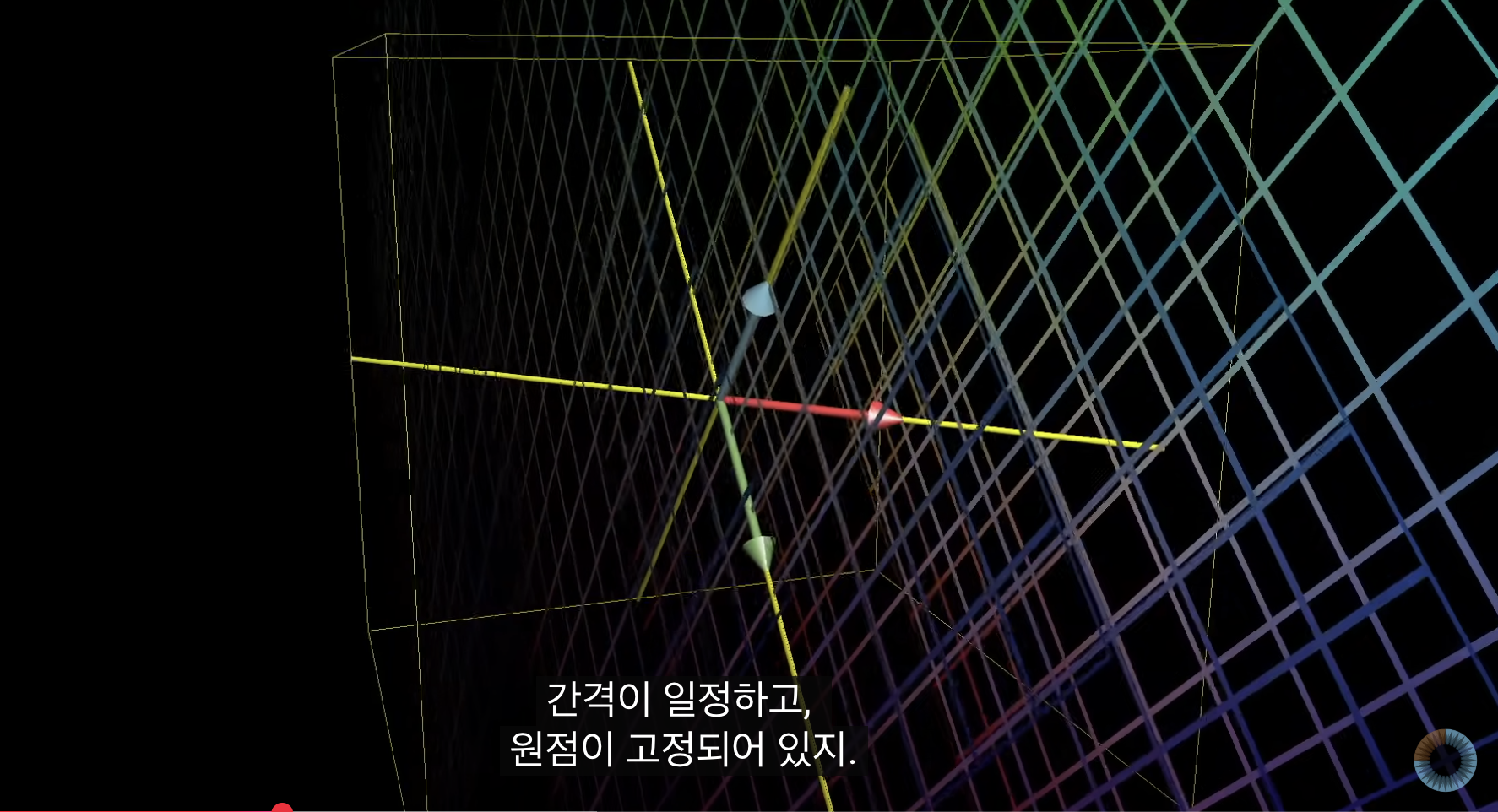
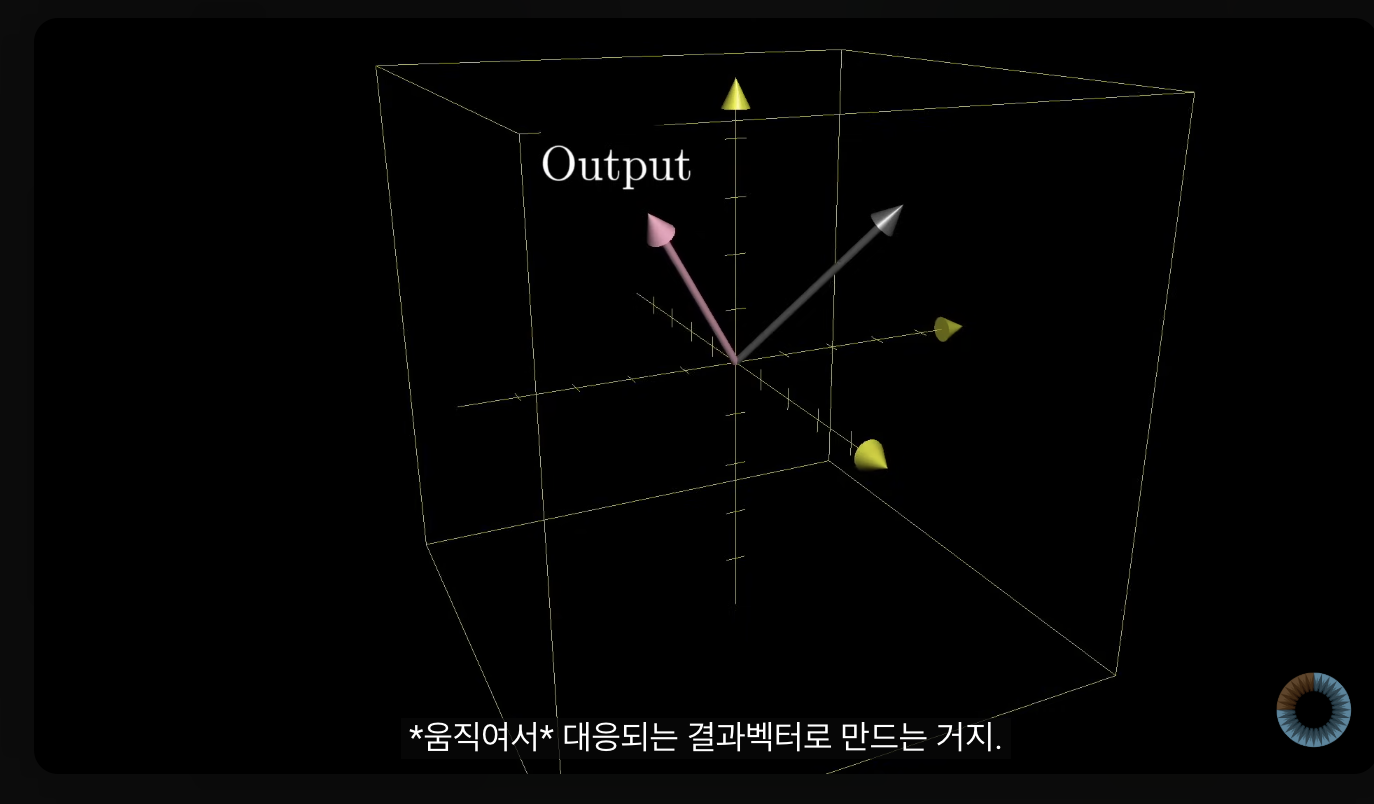
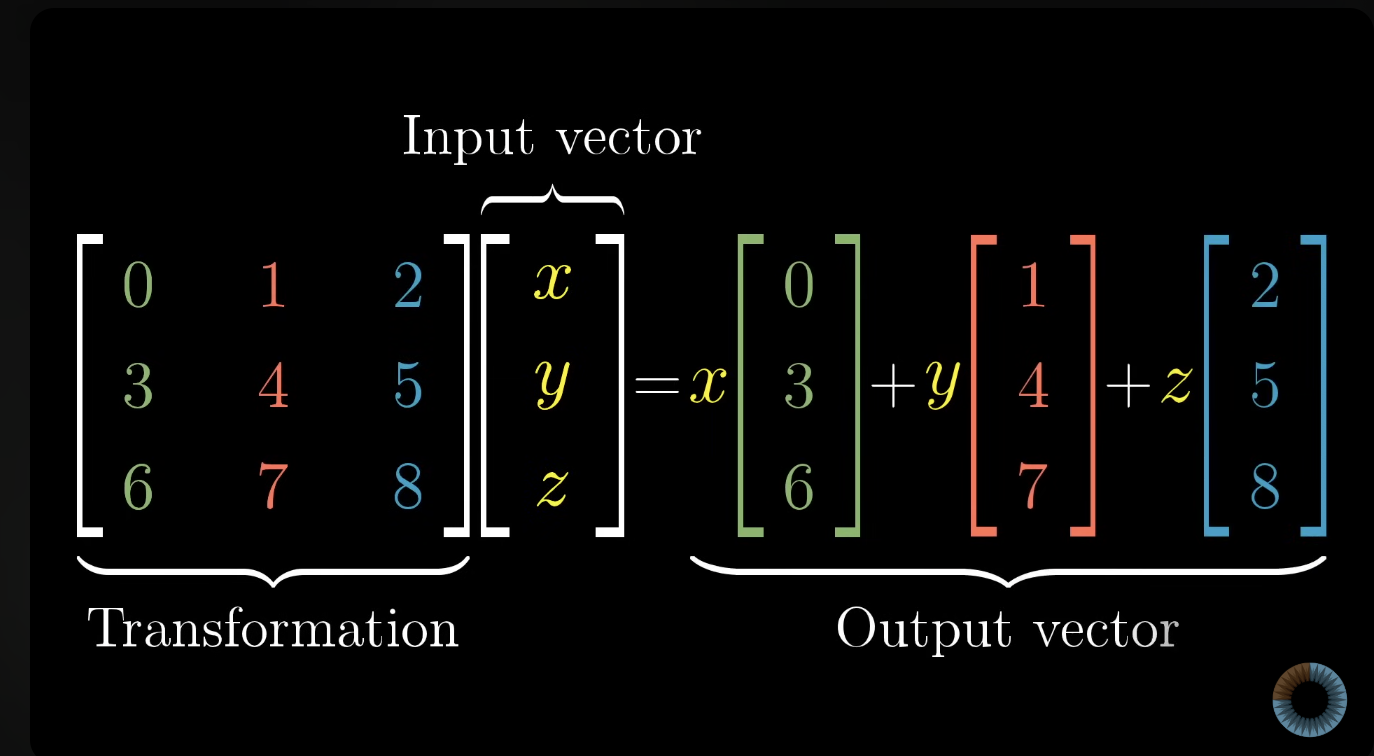
- 2차원과 마찬가지로 벡터의 끝을 공간의 점이라고 생각하고
imput 데이터를 넣고 움직여서 output 데이터를 결과 벡터로 만드는 것
[3개의 표준 기저벡터 표시 방법]
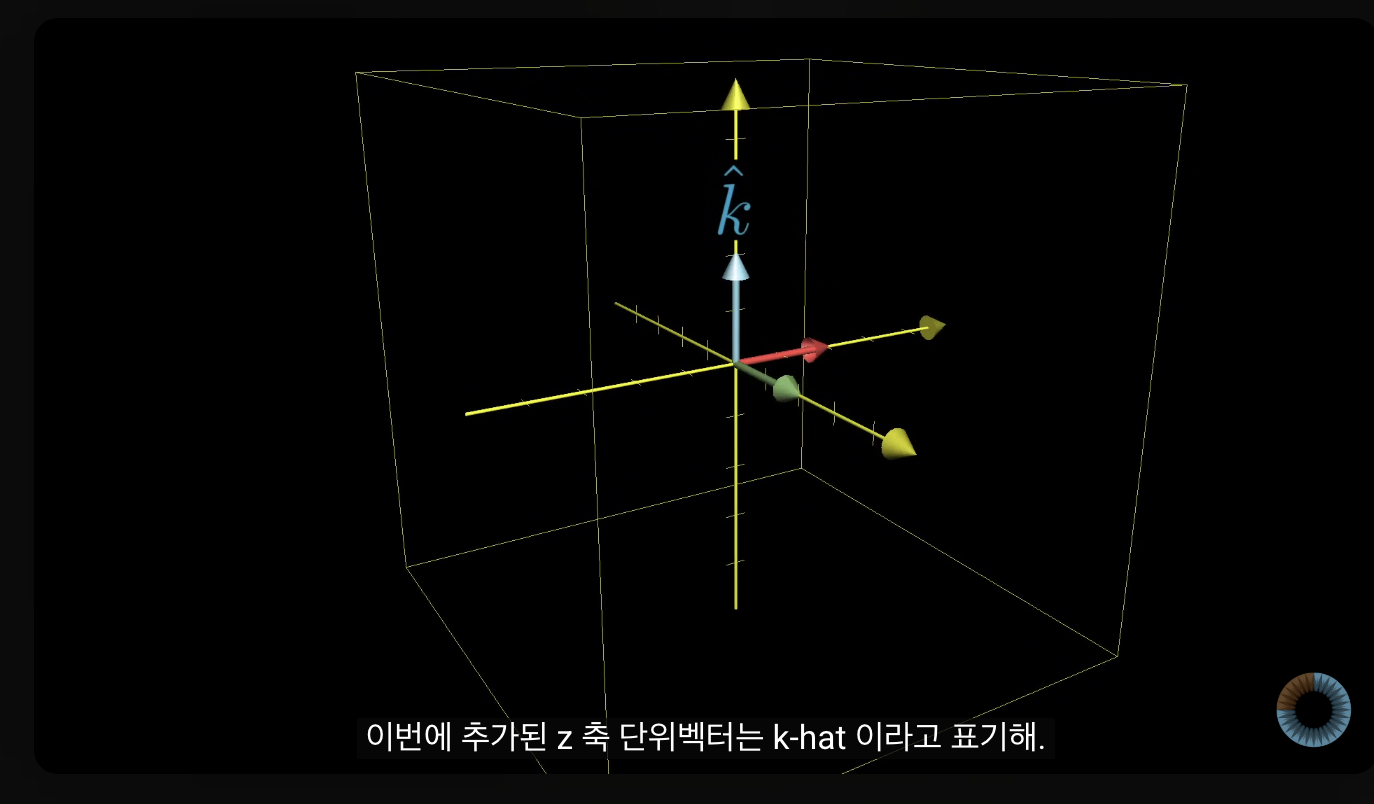
- x 축 방향 단위 벡터 -> i^
- y 축 방향 단위 벡터-> j^
- z축 단위 벡터 -> k^
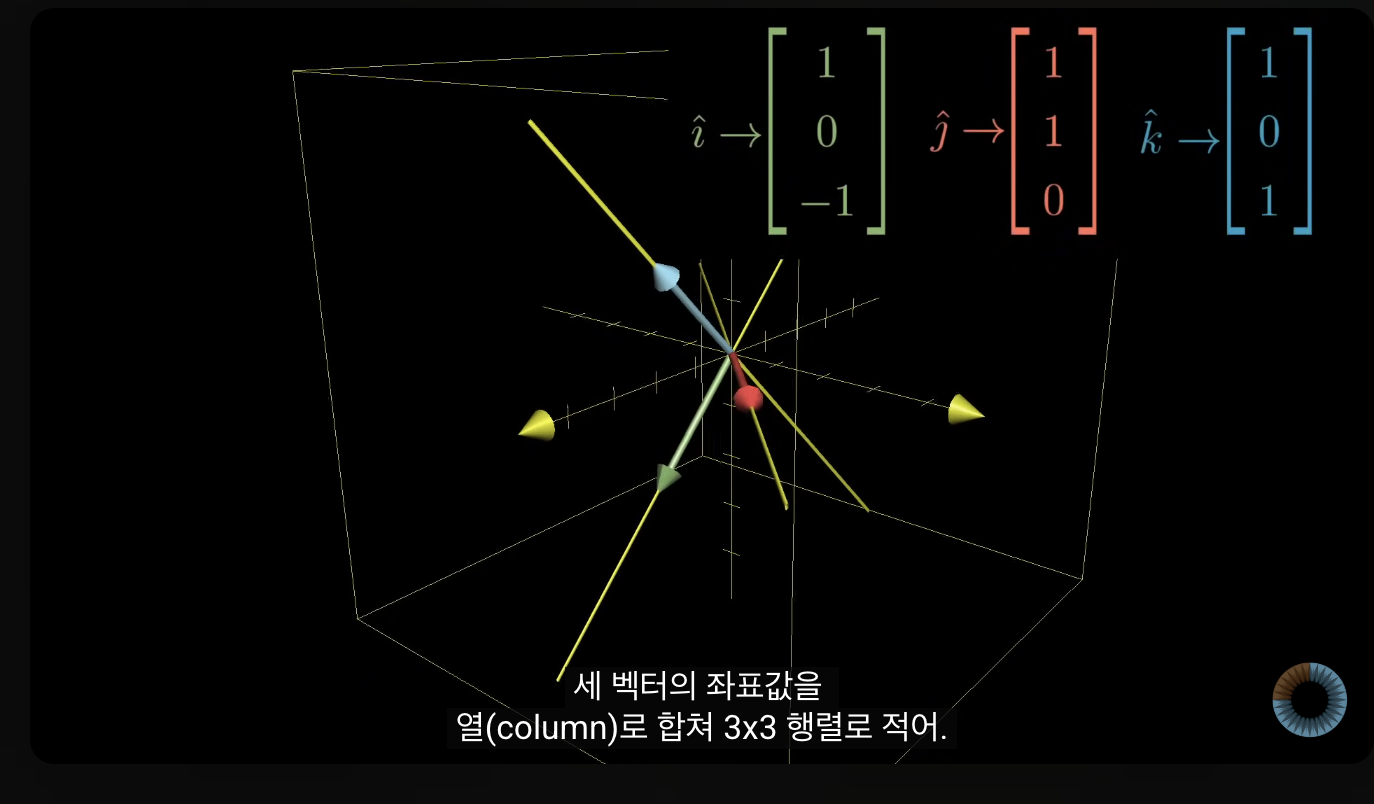
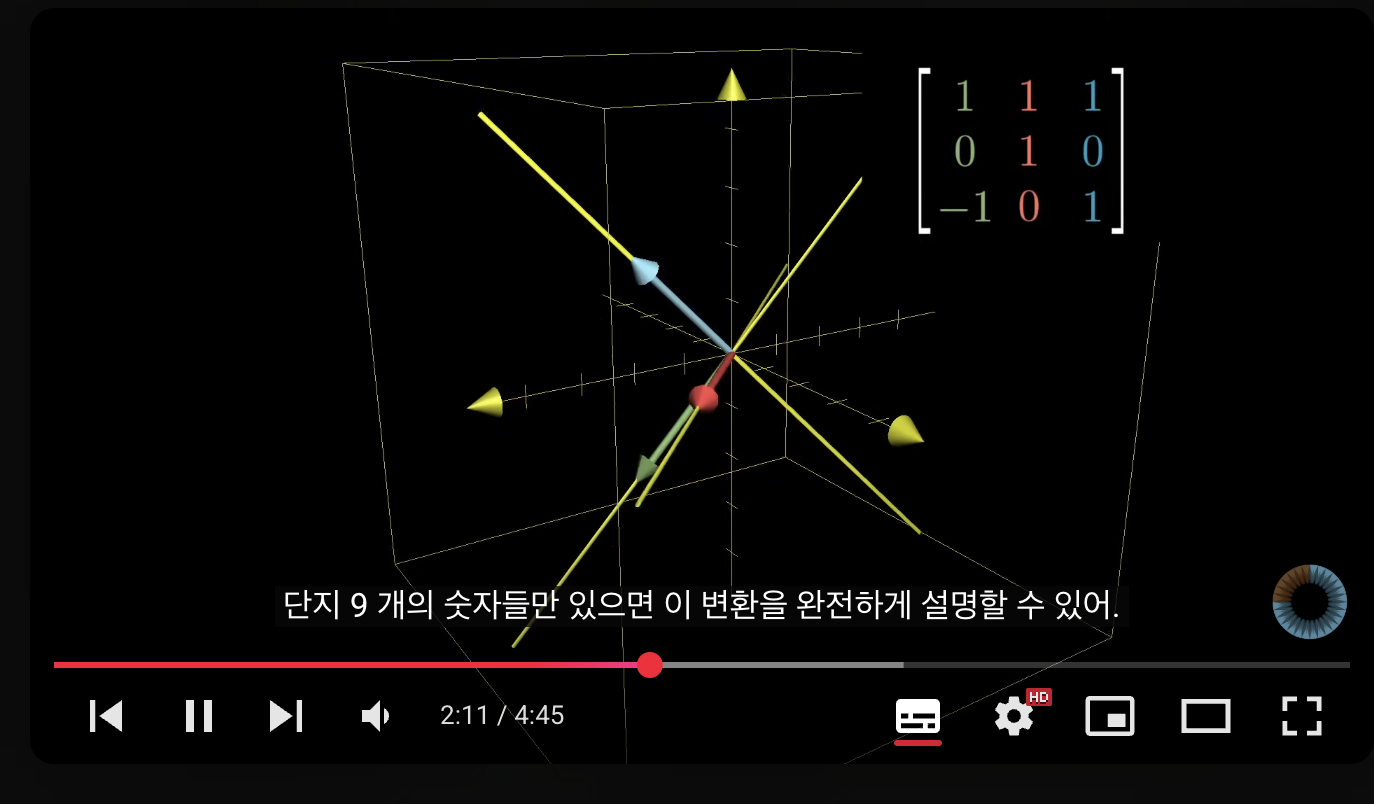
- 세 벡터의 좌표값을 열로 합쳐서 3x3 행렬을 만듦
-> [i^ j^ k^] 순서대로임.
- 아래는 y축을 기준으로 90도 회전시킴
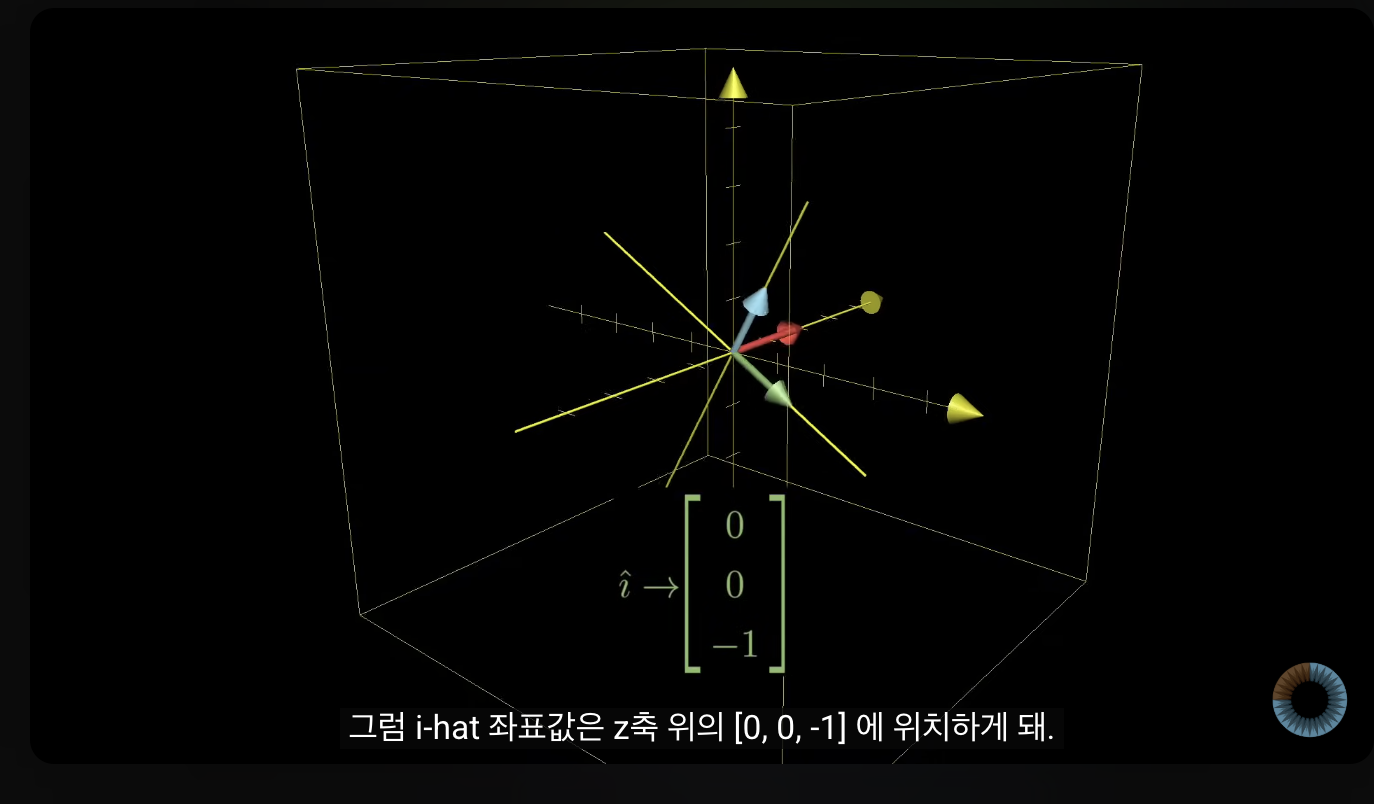
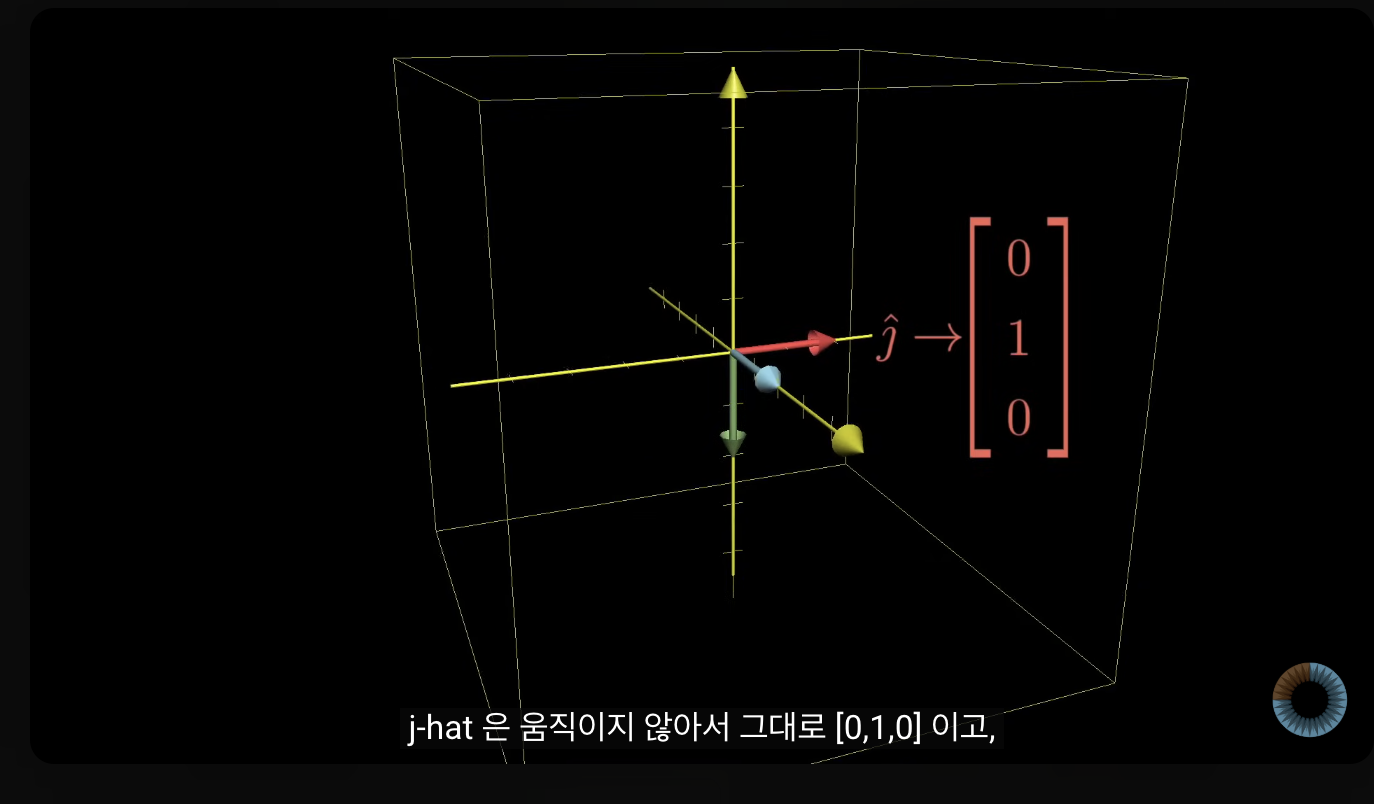
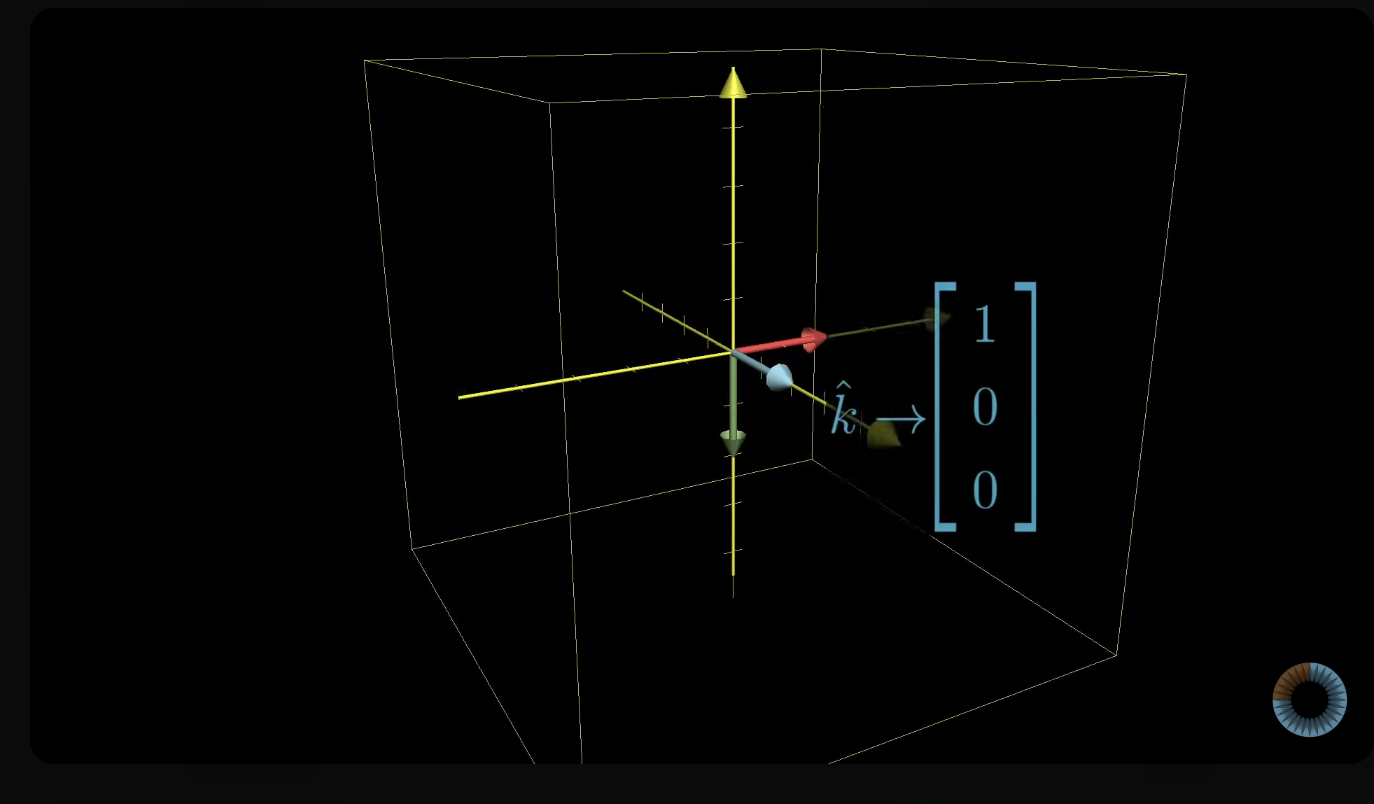
- i^, k^의 값은 바뀌지만 j^은 y축이 움직이지 않아서 바뀌지 않음.
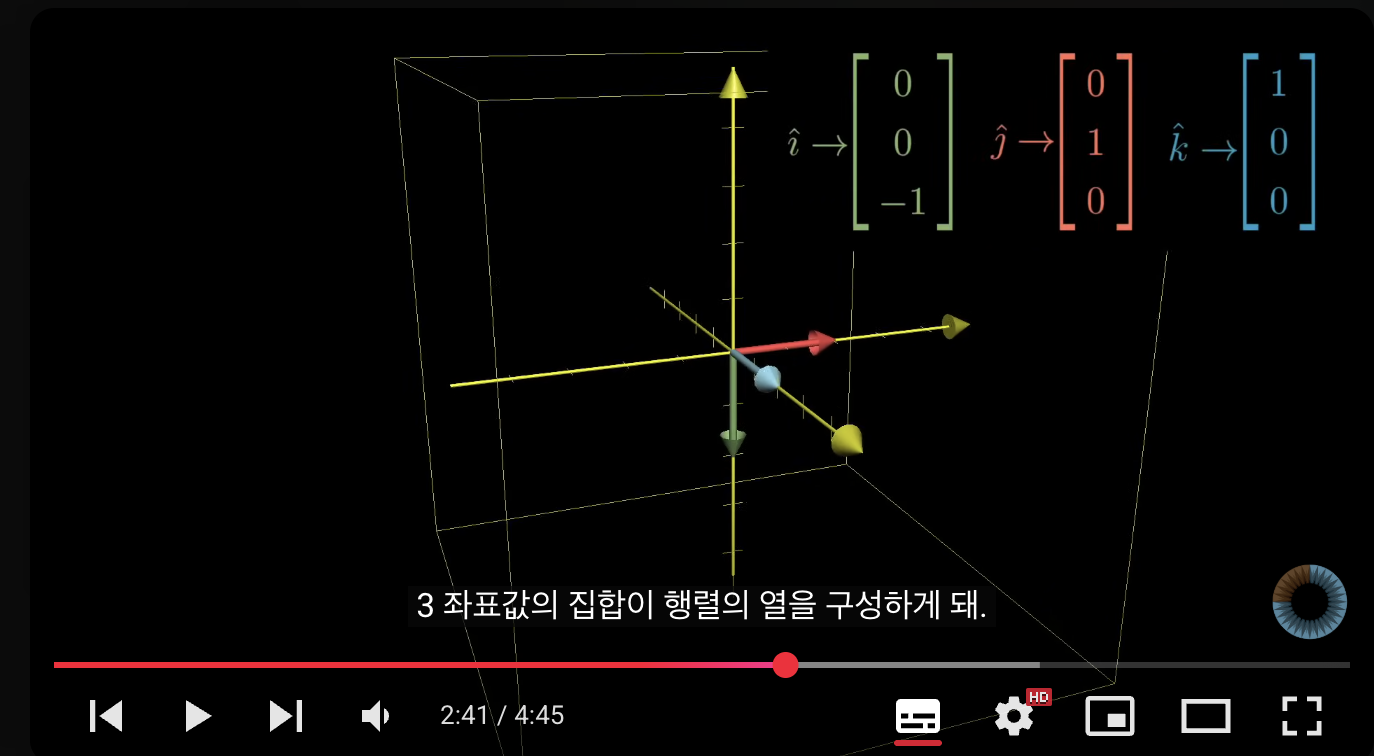
- 아래 값이 회전 변환의 좌표가 되는 것.
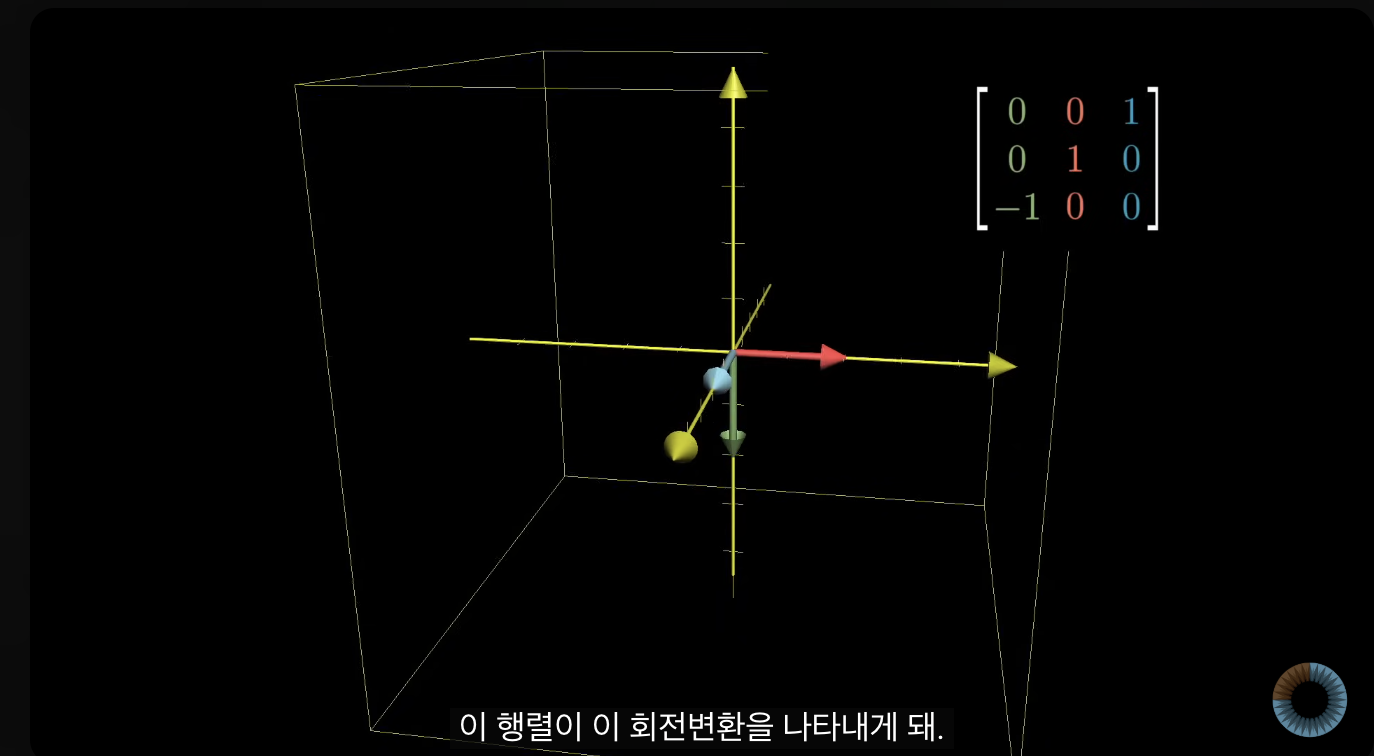
- 2d 일때랑 마찬가지로 각 좌표값은 스케일링 벡터라고 보면 됨.
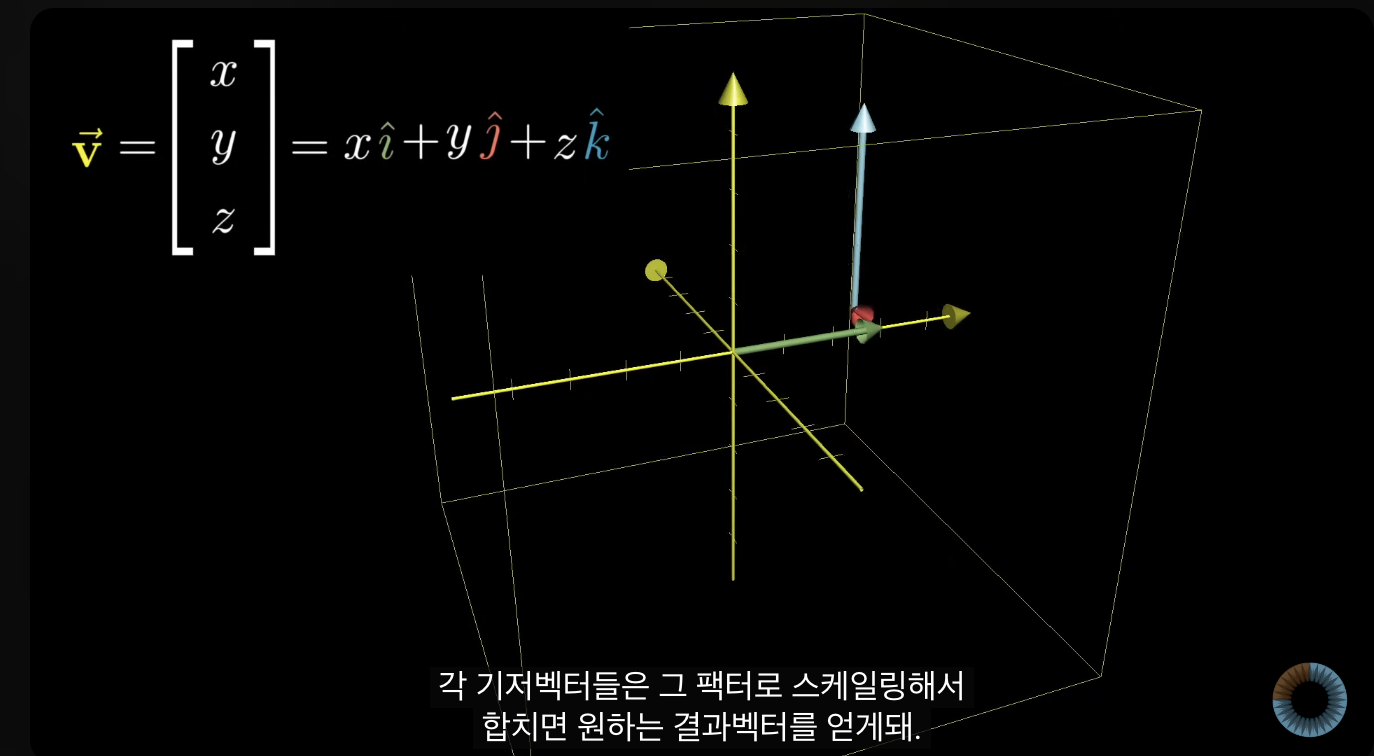
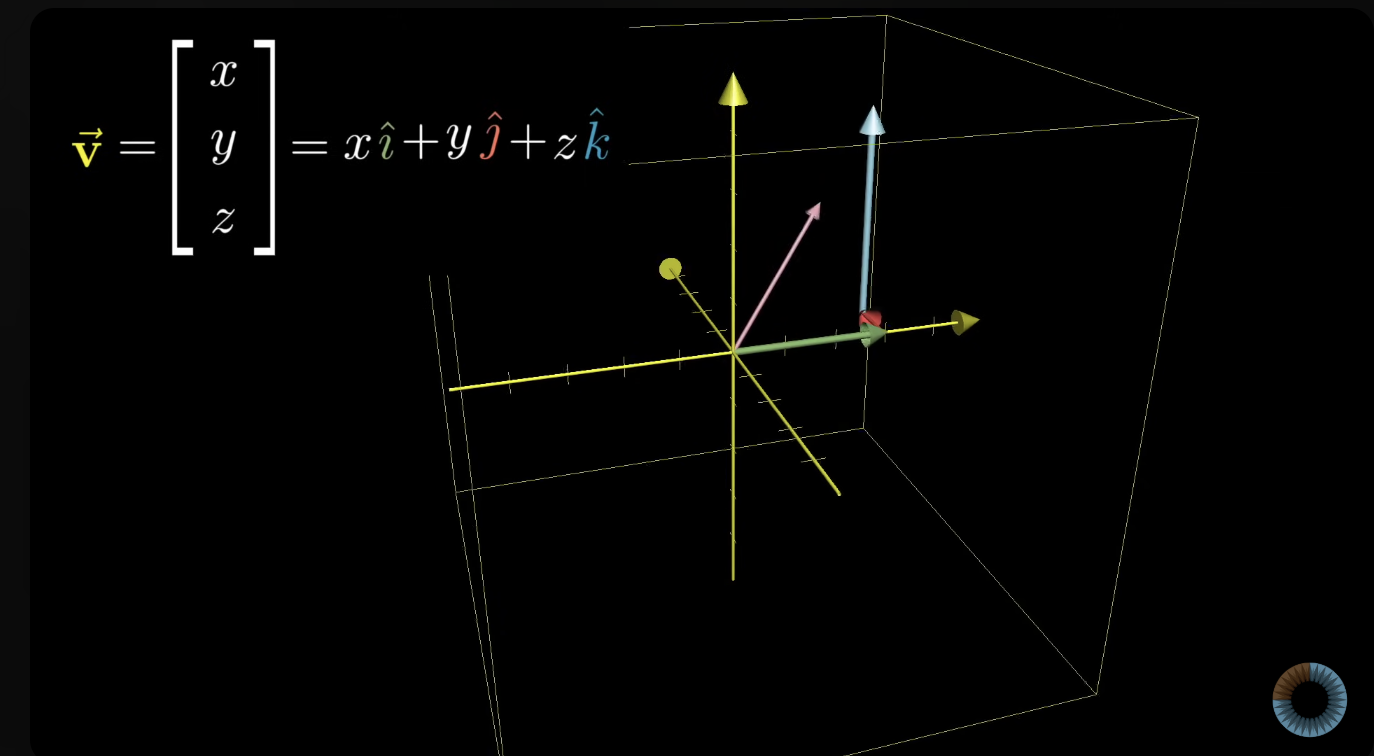
++ 기저벡터에 스케일링과 더하는 절차가 변환 전/후에도 같음. -> 기저 벡터의 수는 선형변환 되는 값이 아닌 ^인 유일 값이니깐..?
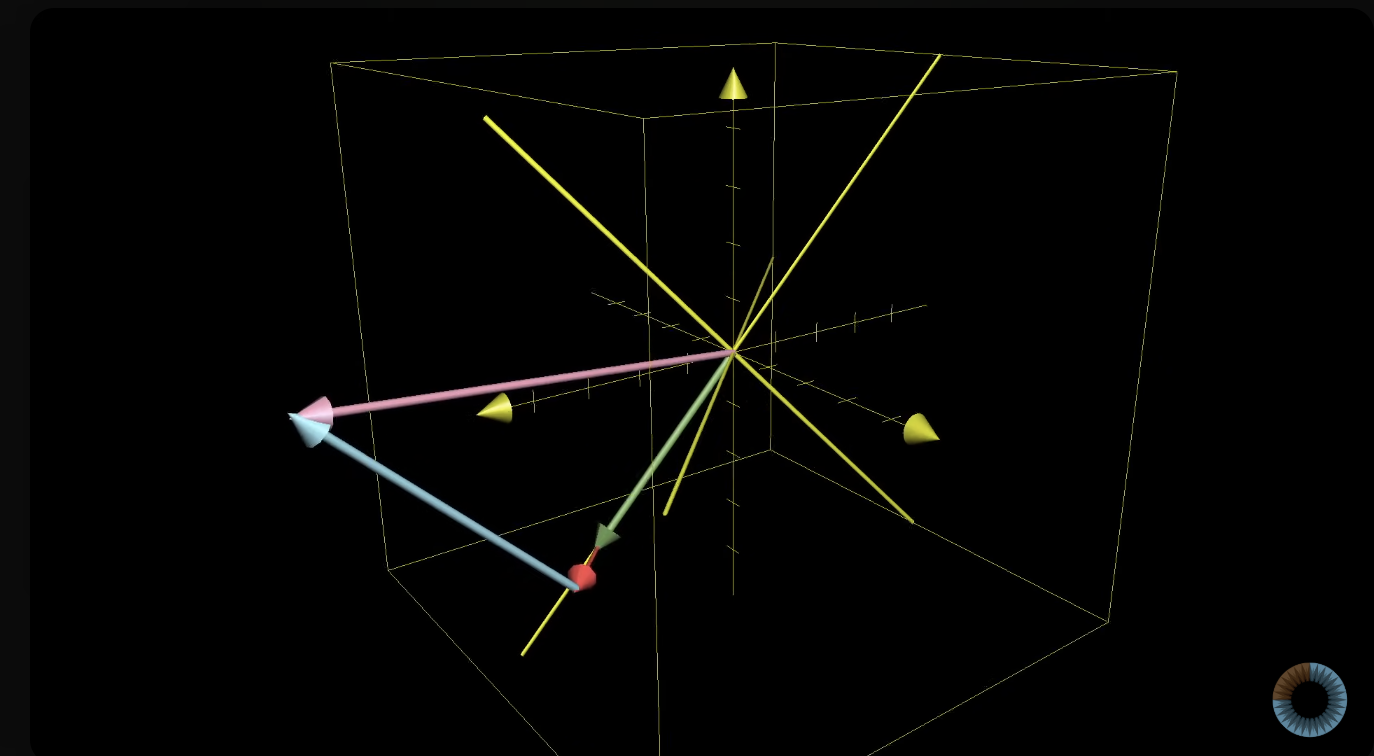
- 아래처럼 고유한 기울기라고 볼 수도 있는 기저벡터들은 변화지 않고, 더하거나 곱하기만 할 뿐임.
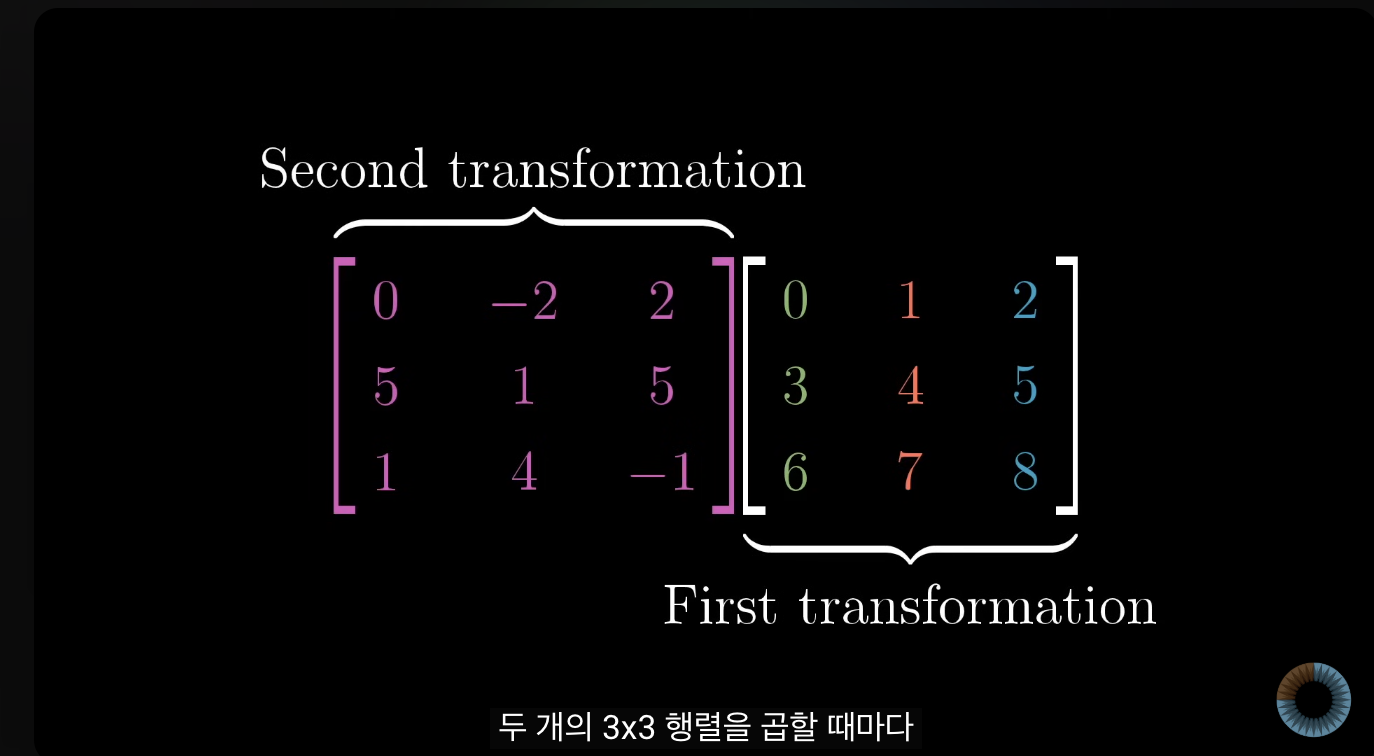
- 두 행렬 곱에서는 마찬가지로 오른쪽부터 계산이 되어서
- 오른쪽으로 행렬 변환이 먼저 일어나고, 왼쪽의 것이 두 번째 것으로 일어남.
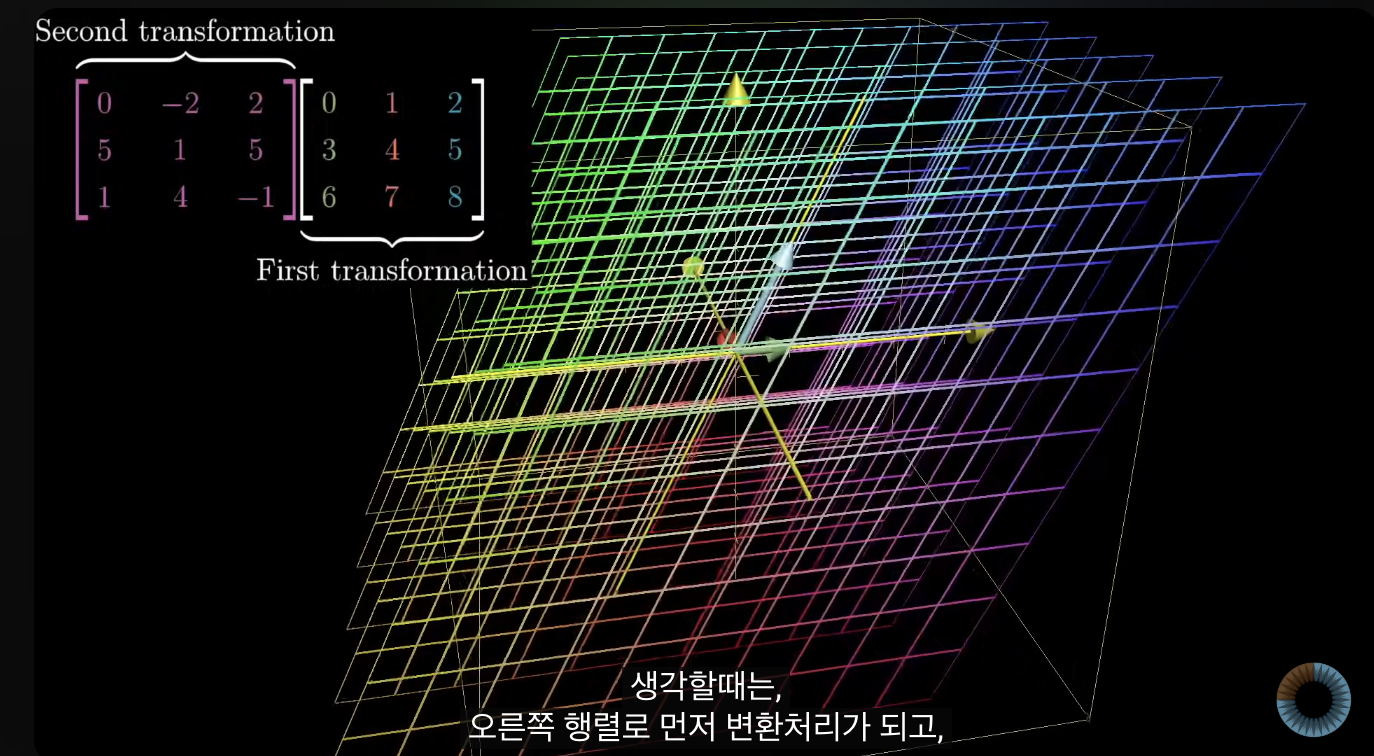
-> 컴퓨터 그래픽이나, 로봇 공학에서 많이 사용함.
-> 선형결합으로 잘라서 결합composition을 하면 이해가기가 더 쉬워짐.
- 행렬 곱을 어떻게 할 지를 고민해보래.. => 이게 자꾸 헷갈림..
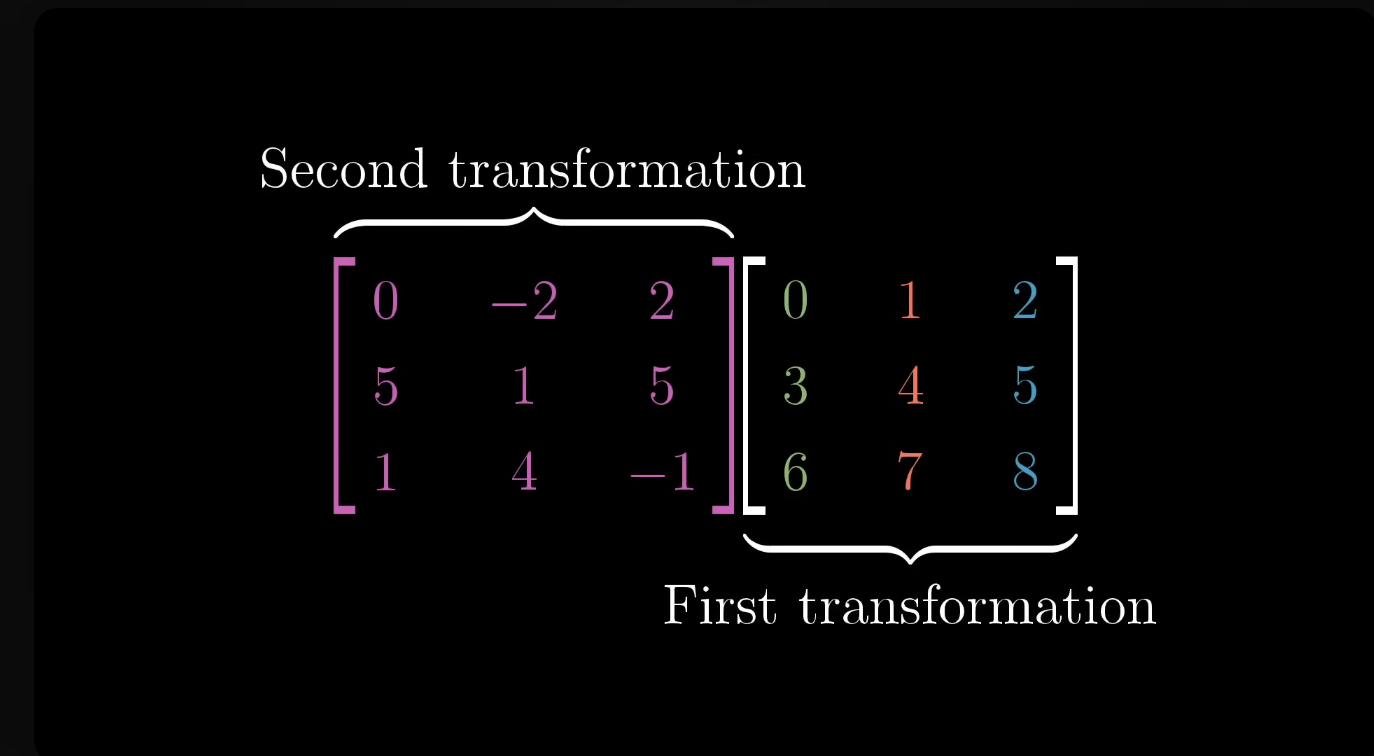
=> 이전 것 보고 해결함!

- 맞긴 했는데..? gpt는 순서를 다르게 곱해서 다른 값이 나오니깐 주의할 것.
- 나는 손으로 계산하고 gpt 에게 검산했음.
'AI > Linear Algebra, Math' 카테고리의 다른 글
| [Essence of linear algebra] ch.7 Inverse matrices, column space and null space (0) | 2025.05.23 |
|---|---|
| [Essence of linear algebra] ch.6 The determinant (0) | 2025.05.11 |
| [Essence of linear algebra] ch4. Matrix multiplication as composition (0) | 2025.05.06 |
| [elice 머신러닝] 통계분석 (0) | 2025.05.04 |
| [elice 머신러닝] 확률 변수와 조건부 확률 (0) | 2025.05.04 |