[elice 통계] 논리적 자료의 요약(평균, 중간값, 최빈값, 분산, 사분위수, cv, 도수분포표)

*elice 강의안

 

- 이미 통계에 많이 접한 사람들은 저런 낚는 용에 넘어가지 않음. 

 

- 모수는 다른 것이 될 수도 있지만, 중심위치와 퍼진 정도를 중요하게 생각함. 

- so, 양 극단(최대, 최소)를 빼고 평균을 내기도 함. 

- 새로 들어온 값 있을 때마다 다시 확인해야 하기 때문에 잘 사용하지 않음.

- 특히, 데이터 값이 많을 수록 자주 사용하지 않음. 

- 최빈값은 넘파이에 없음. scipy의 stats를 가지고 와야 함. 

- stats.mode()

import numpy as np
from scipy import stats

coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])

# 최빈값 계산
cf_mode = stats.mode(coffee)
print("Mode :", cf_mode[0][0]) #[0][0] 일 때는 값을 볼 수 있고
#[1][0]하면 몇 번 나왔는지 빈도를 알 수 있음.

---

- 편차: 양궁선수 < 아마추어 <  일반인. 라고 생각하면 편함. 

- 편차의 합이 0이기 때문에 절대값을 사용하는 방법도 있지만, 대개 편차를 제곱해서 합함.

- 2와 3이 둘 다 20 백분위수에 들어갈 수 있기 때문에 2개를 더해서 평균을 해줄 수 있음. 

-> 2는 20% 지점이고 3이 80% 지점이기 때문에 엄밀히 말해서 둘 다 되는 것. 

- 정수가 아닌 경우는 1을 더한 값 m을 구하고, m번째로 작은 관측값임. 

- IQR=  작은 그룹의 중앙값과 큰 그룹의 중앙값 사이의 거리

- 범위는 안 봐도 됌

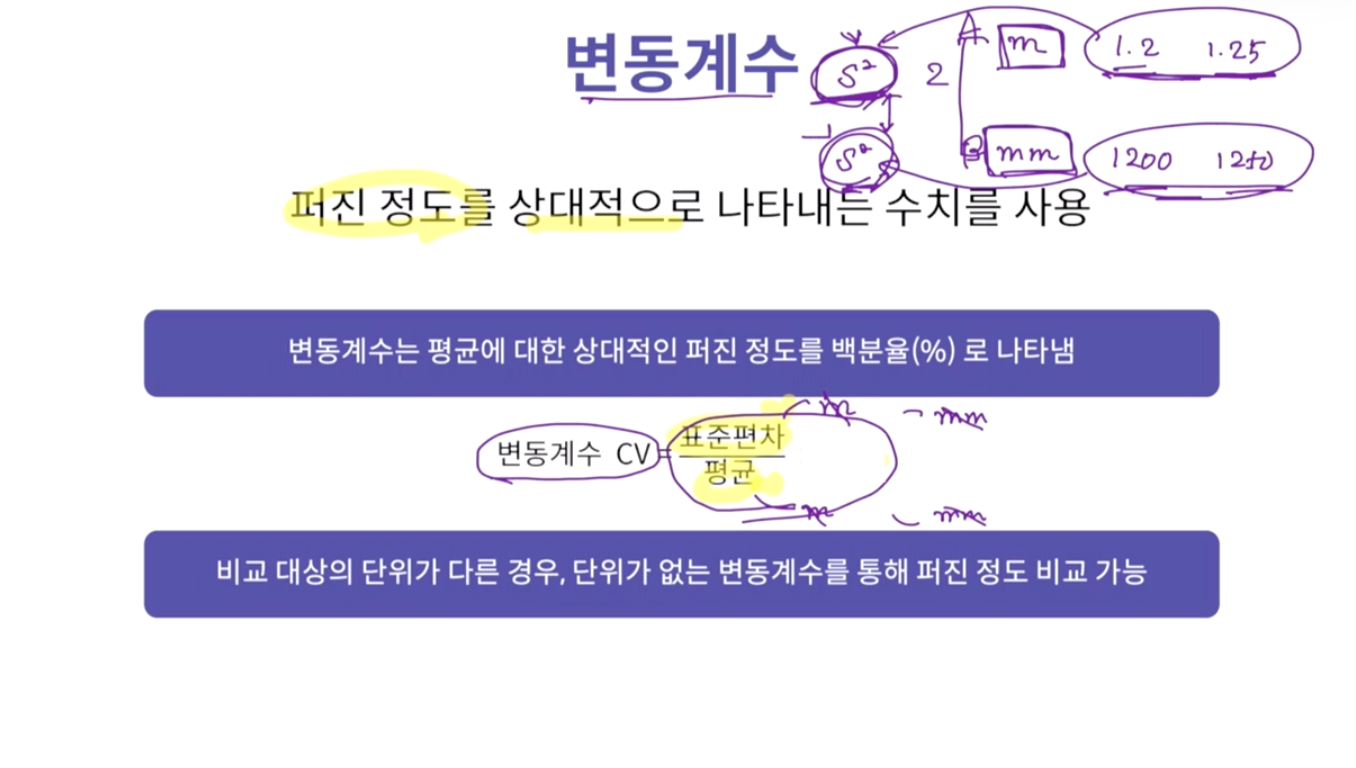
- 즉, 같은 단위의 값을 나눠준 거니깐, 결국 단위가 사라짐.

- 정확한 원자료가 없고 도수분포표만 있을 때도 

 

- 분산 첫번째 식 , 아니고 - 임

import numpy as np
import pandas as pd

# 주량 데이터
drink_cup = pd.DataFrame({
    "cup": [22, 7, 19, 3, 10, 8, 19, 7, 15, 9, 35, 5], 
    "who": ["A", "E", "D", "B", "C", "A", "A", "A", "D", "B", "C", "B"]
})

print(drink_cup)

# 도수분포표
factor_cup = pd.cut(drink_cup.cup, 4) #구간을 4개로 만드는 것
group_cup = drink_cup["cup"].groupby(factor_cup) #나눈 것으로 그룹화
count_cup = group_cup.agg(["count"]) #그룹별로 결과 확인 agg, "count"를 명령어로 쓰는 게 웃김. 

print(count_cup)

############################              
cup           count            
(2.968, 11.0]      7   # ( 초과, ] 이하
(11.0, 19.0]       3
(19.0, 27.0]       1