[Essence of linear algebra] ch.6 The determinant
https://www.youtube.com/watch?v=Ip3X9LOh2dk&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=6
"The purpose of computation is insight, not numbers."
- Richard Hamming
“계산의 목적은 숫자가 아니라 통찰이다.”
또는
“계산의 목적은 통찰이지, 단순한 숫자가 아니다.”
- 오늘의 문장임. 계산의 목적이 결국 쉽게 이해하게 돕기 위한 수단인데.. 너무 반전되어 있다..
- 학창시절에 수학을 하긴 하면서도.. 버렸던 이유가 이해와 계산은 별개였기 때문이다.
- 어제 시간이 떠서 한 번 들었는데.. 여러 번 들을 수록 이해가 잘 되서 지금 들으면서 정리하려고 한다.
[determinant, 행렬식]
- 어떤 경우는 확장하거나 축소하기 때문에 어떨 때 그러는 지 도움이 됨.

- 스케일이 되는 factor 값을 측정해보고자 하는 것. -> 넓이라고 생각해보면 좋음

- 아래 같은 벡터가 있다고 할 때

- 그냥 1x1 정사각형을 생각해보고

- 1인 영역이 2x3 = 6으로 바뀐 것으로 이해하면 됨. => 확장시킨 것


- shear의 경우에는 변환으로 영역이 변화하는 것 같아도 그렇지 않음.
-> 단위 정사각형에서는

- 하나의 정사각형 유닛이 어떻게 변하는지 알면 모든 게 어떻게 변화되는 지 알 수 있음.



=> 크기와 상관없이 격자선이 평행하고 균등한 거리를 유지한 채 변화하기 때문
- 사각형이 아닌 경우, 사각형을 유사하게 매우 작게 만들어내면 근사치를 구할 수 있음.


- 사각형이 아닌 영역도 결국 작은 사각형으로 쪼갤 수 있고, 이는 한 사각형 유닛에 비례한다는 것과 정확히 같은 말임


- determinant 값에 따라서 행렬의 영역 값의 변화를 알 수 있음.

- det = 3이면 3배 커진 것

- 이 경우는 1/2로 줄어든 것
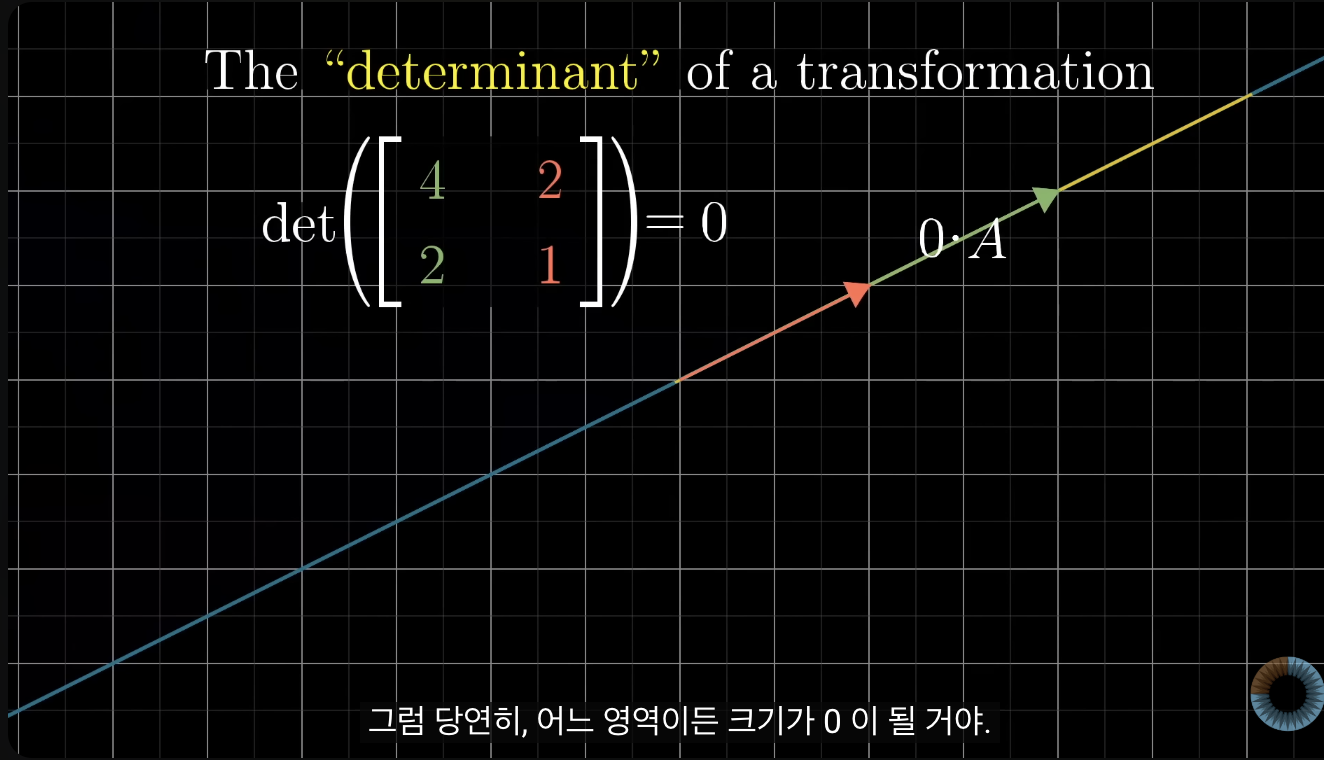
- 만약에 det = 0이 된다면, 선이 되었거나, 극단적으로 .(점)이 된 상태임
-> 즉 0이 된 상태는 계산이 안 되는 상태로 모든 것이 더 작은 차원이 된 상태임

- 음수 값은 방향(orientation)과 연관됨.

- 종이라고 생각하면 종이를 뒤집는 것과 같음
- i^, j^으로도 설명이 가능함

- 처음 시작될때 두 벡터의 위치를 보면, i^의 왼쪽에 j^이 있음.

- 변환된 이후에 j^이 i^의 오른쪽 에 있는 것으로 변화됨.
-> 공간의 방향이 반전된 것.
- 음수 행렬식은 공간이 반전된 것을 의미함. -> 영역의 넓이는 그대로 절대값임.



- 방향이 바뀌고 영역 값은 3배가 된 것
- i^의 값을 점점 움직이면서 det 값을 줄여보면 아래처럼 쪼그라듬

- 0 이 되면 선이됨


- i^이 계속 음수가 되면서 방향 전환이 끝나고 다시 면적이 커짐.
-> 방향이 전환되면 음수 det가 나옴
[3차원 행렬식]
- 부피가 얼마나 스케일링되는 지를 알려줌.

- 2차원 때처럼 큐브(1x1x1) 1개를 생각하면 쉬움


- 정육면체가 기울이고 기울여짐
- Parallelepiped => 평행육면체


- 그려진 정육면체의 부피가 1이었기에 행렬식을 평행육면체 부피 값이라고 생각해도 됨.

- det = 0 일 때 행렬의 열들은 선형의존이 일어남.
-> 평면이나 선이 됨.
-> 하나가 나머지 둘의 선형결합으로 표현될 수 있기 때문

- 3차원에서의 방향은 오른손을 접어서 알 수 있음. 딱 그림처럼.

- 음수로 변환이 일어나면, 왼손으로 바꿔서 확인해야함.

[공식]



=> b or c 중 1개만이라도 0이면, ad 가 행렬식의 값임
- 만약, bc가 0이 아니면, 평행사변형이 얼마나 늘려지거나, 찌그러졌는지 알려줌.


- 3차원도 공식이 있음

- 아래를 증명해볼 것.

🔍 한 문장 설명:
행렬곱 M₁M₂는 두 선형변환을 연달아 적용한 것이므로, 전체 부피 변화율은 각 행렬의 부피 변화율(=행렬식)을 곱한 것과 같다.
📐 직관적으로 보면:
- det(M)은 선형변환이 단위 부피를 얼마나 스케일링하는가를 나타냅니다.
- M₂로 먼저 변환하면 부피가 det(M₂)배 되고,
그 결과에 M₁을 적용하면 다시 det(M₁)배 되니까
전체는 det(M₁)·det(M₂)배가 됩니다.
=> 나는.. 수학자는 못 될듯.. 확 와닿지가 않는다...